BRICS Lecture Series, Abstracts, 1995-98

March 4, 2002

This document is also available as PostScript, DVI, Text.

Bibliography

LS-01-1
PostScript, PDF, DVI.
Zsolt Tuza.
Unsolved Combinatorial Problems, Part I.
May 2001.
viii+30 pp.
Abstract:

<

#43#>Contents
1
Subset-Sums Equality
2
Boolean Satisfiability and Hypergraph 2-Coloring with bounded degrees
3
Second Hamiltonian Cycle
4
The number of Hamiltonian subgraphs
5
Local vs. global average degree in graphs
6
Uniform edge cover with triangles
7
Single Input Double Output controllers
8
Ryser's conjecture on 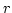$r$-partite hypergraphs
9
Covering the triangles with edges
10
Largest bipartite subgraphs of graphs
11
Weighted edge covering with complete subgraphs
12
Strongly triangle-free subgraphs
13
Excluded cycle lengths, chromatic number, and orientations
14
The Acyclic Orientation Game
15
Transversals of uniform hypergraphs
16
Covering and coloring the maximal complete subgraphs
.

LS-98-4
PostScript, PDF, DVI.
Paola Quaglia.
The $\pi$-Calculus: Notes on Labelled Semantics.
December 1998.
viii+16 pp.
Abstract: The $\pi$-calculus is a name-passing calculus that allows the description of distributed systems with a dynamically changing interconnection topology. Name communication, together with the possibility of declaring and exporting local names, gives the calculus a great expressive power. For instance, it was remarkably shown that process-passing calculi, that express mobility at higher order, can be naturally encoded in $\pi$-calculus.

Since its very first definition, the $\pi$-calculus proliferated in a family of calculi slightly departing the another either in the communication paradigm (polyadic vs monadic, asynchronous vs synchronous) or in the bisimulation semantics (labelled vs unlabelled, late vs early vs open vs barbed vs ...).

These short notes present a collection of the labelled strong semantics of the (synchronous monadic) $\pi$-calculus. The notes could not possibly substitute any of the standard references listed in the Bibliography. They rather represent an attempt to group together, using a uniform notation and the terminology that got assessed over the last years, a few definitions and concepts otherwise scattered throughout the $\pi$-calculus literature.

<

#56#>Contents
1
Preliminaries
2
Syntax
3
Labelled semantics
3.1
Late semantics
3.2
Early semantics
3.3
Open semantics
.

LS-98-3
Olivier Danvy.
Type-Directed Partial Evaluation.
December 1998.
Extended version of lecture notes to appear in.
Abstract: Type-directed partial evaluation uses a normalization function to achieve partial evaluation. These lecture notes review its background, foundations, practice, and applications. Of specific interest is the modular technique of offline and online type-directed partial evaluation in Standard ML of New Jersey.

<

#64#>Contents
1
Background and introduction
1.1
Partial evaluation by normalization
1.2
Prerequisites and notation
1.3
Two-level programming in ML
1.4
Binding-time coercions
1.5
Summary and conclusion
2
Normalization by evaluation
2.1
A normalization function
2.2
Application to decompilation
2.3
Normalization by evaluation
2.4
Naive normalization by evaluation in ML
2.5
Towards type-directed partial evaluation
2.6
Normalization by evaluation in ML
2.7
Summary and conclusion
3
Offline type-directed partial evaluation
3.1
The power function, part 1
3.2
The power function, part 2
3.3
Summary and conclusion
4
Online type-directed partial evaluation
4.1
Online simplification for integers
4.2
The power function, revisited
4.3
Summary and conclusion
5
Incremental type-directed partial evaluation
6
Conclusion and issues
.

LS-98-2
PostScript, PDF, DVI.
Carsten Butz.
Regular Categories and Regular Logic.
October 1998.
Abstract: Notes handed out to students attending the course on Category Theory at the Department of Computer Science in Aarhus, Spring 1998. These notes were supposed to give more detailed information about the relationship between regular categories and regular logic than is contained in Jaap van Oosten's script on category theory (BRICS Lectures Series LS-95-1). Regular logic is there called coherent logic.

<

#85#>Contents
1
Prologue
2
Regular Categories
3
Regular Logic
4
A Sound Calculus
5
The Internal Logic of a Regular Category
6
The Generic Model of a Regular Theory
7
Epilogue
.

LS-98-1
PostScript, PDF, DVI.
Ulrich Kohlenbach.
Proof Interpretations.
June 1998.
Abstract: These lecture notes are a polished version of notes from a BRICS PhD course given in the spring term 1998.

Their purpose is to give an introduction to two major proof theoretic techniques: functional interpretation and (modified) realizability. We focus on the possible use of these methods to extract programs, bounds and other effective data from given proofs.

Both methods are developed in the framework of intuitionistic arithmetic in higher types.

We also discuss applications to systems based on classical logic. We show that the combination of functional interpretation with the so-called negative translation, which allows to embed various classical theories into their intuitionistic counterparts, can be used to unwind non-constructive proofs.

Instead of combining functional interpretation with negative translation one can also use in some circumstances a combination of modified realizability with negative translation if one inserts the so-called A-translation (due to H. Friedman) as an intermediate step.

<

#98#>Contents
1
Introduction: Unwinding proofs
2
Intuitionistic logic and arithmetic in all finite types
3
Modified realizability
4
Majorizability and the fan rule
5
Gödel's functional (`Dialectica-')interpretation
6
Negative translation and its use combined with functional interpretation
7
The Friedman A-translation
8
Final comments
.

LS-97-1
PostScript, PDF, DVI.
Jan Chomicki and David Toman.
Temporal Logic in Information Systems.
November 1997.
viii+42 pp. Full version to appear in: Logics for Database and Information Systems, Chomicki and Saake (eds.), Kluwer Academic Publishers, 1998.
Abstract: Temporal logic is obtained by adding temporal connectives to a logic language. Explicit references to time are hidden inside the temporal connectives. Different variants of temporal logic use different sets of such connectives. In this chapter, we survey the fundamental varieties of temporal logic and describe their applications in information systems.

Several features of temporal logic make it especially attractive as a query and integrity constraint language for temporal databases. First, because the references to time are hidden, queries and integrity constraints are formulated in an abstract, representation-independent way. Second, temporal logic is amenable to efficient implementation. Temporal logic queries can be translated to an algebraic language. Temporal logic constraints can be efficiently enforced using auxiliary stored information. More general languages, with explicit references to time, do not share these properties.

Recent research has proposed various implementation techniques to make temporal logic practically useful in database applications. Also, the relationships between different varieties of temporal logic and between temporal logic and other temporal languages have been clarified. We report on these developments and outline some of the remaining open research problems.

<

#111#>Contents
1
Introduction
2
Temporal Databases
2.1
Abstract Temporal Databases
2.2
Relational Database Histories
3
Temporal Queries
3.1
Abstract Temporal Query Languages
3.2
Expressive Power
3.3
Space-efficient Encoding of Temporal Databases
3.4
Concrete Temporal Query Languages
3.5
Evaluation of Abstract Query Languages using Compilation
3.6
SQL and Derived Temporal Query Languages
4
Temporal Integrity Constraints
4.1
Notions of constraint satisfaction
4.2
Temporal Integrity Maintenance
4.3
Temporal Constraint Checking
5
Multidimensional Time
5.1
Why Multiple Temporal Dimensions?
5.2
Abstract Query Languages for Multi-dimensional Time
5.3
Encoding of Multi-dimensional Temporal Databases
6
Beyond First-order Temporal Logic
7
Conclusion
.

LS-96-6
PostScript, PDF, DVI.
Torben Braüner.
Introduction to Linear Logic.
December 1996.
iiiv+55 pp.
Abstract: The main concern of this report is to give an introduction to Linear Logic. For pedagogical purposes we shall also have a look at Classical Logic as well as Intuitionistic Logic. Linear Logic was introduced by J.-Y. Girard in 1987 and it has attracted much attention from computer scientists, as it is a logical way of coping with resources and resource control. The focus of this technical report will be on proof-theory and computational interpretation of proofs, that is, we will focus on the question of how to interpret proofs as programs and reduction (cut-elimination) as evaluation. We first introduce Classical Logic. This is the fundamental idea of the proofs-as-programs paradigm. Cut-elimination for Classical Logic is highly non-deterministic; it is shown how this can be remedied either by moving to Intuitionistic Logic or to Linear Logic. In the case on Linear Logic we consider Intuitionistic Linear Logic as well as Classical Linear Logic. Furthermore, we take a look at the Girard Translation translating Intuitionistic Logic into Intuitionistic Linear Logic. Also, we give a brief introduction to some concrete models of Intuitionistic Linear Logic. No proofs will be given except that a proof of cut-elimination for the multiplicative fragment of Classical Linear Logic is included in an appendix

<

#132#>Contents
1
Classical and Intuitionistic Logic
1.1
Classical Logic
1.2
Intuitionistic Logic
1.3
The 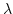$\lambda $-Calculus
1.4
The Curry-Howard Isomorphism
2
Linear Logic
2.1
Classical Linear Logic
2.2
Intuitionistic Linear Logic
2.3
A Digression - Russell's Paradox and Linear Logic
2.4
The Linear 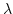$\lambda $-Calculus
2.5
The Curry-Howard Isomorphism
2.6
The Girard Translation
2.7
Concrete Models
A
Logics
A.1
Classical Logic
A.2
Intuitionistic Logic
A.3
Classical Linear Logic
A.4
Intuitionistic Linear Logic
B
Cut-Elimination for Classical Linear Logic
B.1
Some Preliminary Results
B.2
Putting the Proof Together
.

LS-96-5
PostScript, PDF.
Devdatt P. Dubhashi.
What Can't You Do With LP?
December 1996.
viii+23 pp.
Abstract: These notes from the BRICS course ``Pearls of Theory'' are an introduction to Linear Programming and its use in solving problems in Combinatorics and in the design and analysis of algorithms for combinatorial problems.

<

#151#>Contents
1
Dr. Cheng's Diet and LP
2
LP versus NP: A Panacea?
3
Duality
4
Linear versus Integer
5
Luck: Unimodularity
6
Rounding
7
Randomised Rounding
8
Primal-Dual
9
If You Want to Prospect for more Pearls ...
10
Problems
.

LS-96-4
PostScript, DVI.
Sven Skyum.
A Non-Linear Lower Bound for Monotone Circuit Size.
December 1996.
viii+14 pp.
Abstract: In complexity theory we are faced with the frustrating situation that we are able to prove very few non trivial lower bounds. In the area of combinatorial complexity theory which this note is about, the situation can be described quite precisely in the sense that although almost all functions are very complex (have exponential circuit size), no one has been able to prove any non-linear lower bounds for explicitly given functions.

One alley which is often taken is to restrict the models to make larger lower bounds more likely. Until 1985 no non-linear lower bounds were known for monotone circuit size either (the best lower bound was $4n$). In 1985, Razborov [1] proved a super polynomial lower bound for a specific family of Boolean functions.

Razborov proved the following:
Any family of monotone Boolean circuits accepting graphs containing cliques of size $\lfloor{n/2}\rfloor$ has super polynomial size when the graphs are represented by their incidence matrices.
The main purpose of this note is to give a ``simple'' version of Razborov's proof. This leads to a weaker result but the proof contains all the ingredients of Razborov's proof.

We will prove:
Any family of monotone Boolean circuits accepting graphs containing cliques of size 3 (triangles) has size $\Omega(n^3/\log ^4n)$.
In Section 1 we introduce Boolean functions and the complexity model we are going to use, namely Boolean circuits. In Section 2 the appropriate definitions of graphs are given and some combinatorial properties about them are proven. Section 3 contains the proof of the main result.
[1]
A. A. Razborov: Lower bounds on the monotone complexity of some Boolean functions, Dokl. Akad. Nauk SSSR 281(4) (1985) 798 - 801 (In Russian); English translation in: Soviet Math. Dokl. 31 (1985) 354-57.

<

#174#>Contents
1
Boolean functions and circuits
2
Graphs and Combinatorial lemmas
3
Putting things together
4
Problems
.

LS-96-3
PostScript.
Kristoffer H. Rose.
Explicit Substitution - Tutorial & Survey.
September 1996.
v+150 pp.
Abstract: These lecture notes are from the BRICS mini-course ``Explicit Substitution'' taught at University of Aarhus, October 27, 1996.

We give a coherent overview of the area of explicit substitution and some applications. The focus is on the operational or syntactic side of things, in particular we will not cover the areas of semantics and type systems for explicit substitution calculi. Emphasis is put on providing a universal understanding of the very different techniques used by various authors in the area.

<

#185#>Contents
1
Explicit Substitution Rules
1.1
Explicit Substitution
1.2
Preservation of Strong Normalisation (PSN)
1.3
Discussion
2
Explicit Binding
2.1
Namefree 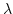$\lambda $-Calculus
2.2
Explicit Binding Variations for Explicit Substitution
2.3
Discussion
3
Explicit Addresses
3.1
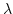$\lambda $-graphs and Explicit Sharing
3.2
Explicit Substitution & Sharing
3.3
Discussion
4
Higher-Order Rewriting and Functional Programs
4.1
Combinatory Reduction Systems (CRS)
4.2
Explicit Substitutes
4.3
Explicit Addresses
4.4
CRS and Functional Programs
4.5
Discussion
5
Strategies and Abstract Machines
5.1
Strategies for 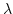$\lambda $-Calculus
5.2
Calculi for Weak Reduction with Sharing
5.3
Reduction Strategies
5.4
Constructors and Recursion
5.5
A Space Leak Free Calculus
5.6
Discussion
A
Appendices: Preliminaries
A.1
Reductions
A.2
Inductive Notations
A.3
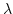$\lambda $-Calculus
.

LS-96-2
PostScript, DVI.
Susanne Albers.
Competitive Online Algorithms.
September 1996.
iix+57 pp.
Abstract: These lecture notes are from the mini-course ``Competitive Online Algorithms'' taught at Aarhus University, August 27-29, 1996.

The mini-course consisted of three lectures. In the first lecture we gave basic definitions and presented important techniques that are used in the study on online algorithms. The paging problem was always the running example to explain and illustrate the material. We also discussed the $k$-server problem, which is a very well-studied generalization of the paging problem.

The second lecture was concerned with self-organizing data structures, in particular self-organizing linear lists. We presented results on deterministic and randomized online algorithms. Furthermore, we showed that linear lists can be used to build very effective data compression schemes and reported on theoretical as well as experimental results.

In the third lecture we discussed three application areas in which interesting online problems arise. The areas were (1) distributed data management, (2) scheduling and load balancing, and (3) robot navigation and exploration. In each of these fields we gave some important results.

<

#208#>Contents
1
Online algorithms and competitive analysis
1.1
Basic definitions
1.2
Results on deterministic paging algorithms
2
Randomization in online algorithms
2.1
General concepts
2.2
Randomized paging algorithms against oblivious adversaries
3
Proof techniques
3.1
Potential functions
3.2
Yao's minimax principle
4
The 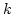$k$-server problem
5
The list update problem
5.1
Deterministic online algorithms
5.2
Randomized online algorithms
5.3
Average case analyses of list update algorithms
6
Data compression based on linear lists
6.1
Theoretical results
6.2
Experimental results
6.3
The compression algorithm by Burrows and Wheeler
7
Distributed data management
7.1
Formal definition of migration and replication problems
7.2
Page migration
7.3
Page replication
7.4
Page allocation
8
Scheduling and load balancing
8.1
Scheduling
8.2
Load balancing
9
Robot navigation and exploration
.

LS-96-1
PostScript, PDF.
Lars Arge.
External-Memory Algorithms with Applications in Geographic Information Systems.
September 1996.
iix+53 pp.
Abstract: In the design of algorithms for large-scale applications it is essential to consider the problem of minimizing Input/Output (I/O) communication. Geographical information systems (GIS) are good examples of such large-scale applications as they frequently handle huge amounts of spatial data. In this note we survey the recent developments in external-memory algorithms with applications in GIS. First we discuss the Aggarwal-Vitter I/O-model and illustrate why normal internal-memory algorithms for even very simple problems can perform terribly in an I/O-environment. Then we describe the fundamental paradigms for designing I/O-efficient algorithms by using them to design efficient sorting algorithms. We then go on and survey external-memory algorithms for computational geometry problems--with special emphasis on problems with applications in GIS--and techniques for designing such algorithms: Using the orthogonal line segment intersection problem we illustrate the distribution-sweeping and the buffer tree techniques which can be used to solve a large number of important problems. Using the batched range searching problem we introduce the external segment tree. We also discuss an algorithm for the reb/blue line segment intersection problem--an important subproblem in map overlaying. In doing so we introduce the batched filtering and the external fractional cascading techniques. Finally, we shortly describe TPIE--a Transparent Parallel I/O Environment designed to allow programmers to write I/O-efficient programs.

These lecture notes were made for the CISM Advanced School on Algorithmic Foundations of Geographic Information Systems, September 16-20, 1996, Udine, Italy.

<

#238#>Contents
1
Introduction
1.1
The Parallel Disk Model
1.2
Outline
2
RAM-Complexity and I/O-Complexity
2.1
Fundamental External-Memory Bounds
2.2
Summary
3
Paradigms for Designing I/O-efficient Algorithms
3.1
Merge Sort
3.2
Distribution Sort
3.3
Buffer Tree Sort
3.4
Sorting on Parallel Disks
3.5
Summary
4
External-Memory Computational Geometry Algorithms
4.1
The Orthogonal Line Segment Intersection Problem
4.2
The Batched Range Searching Problem
4.3
The Red/Blue Line Segment Intersection Problem
4.4
Other External-Memory Computational Geometry Algorithms
4.5
Summary
5
TPIE -- A Transparent Parallel I/O Environment
6
Conclusions
.

LS-95-5
PostScript, DVI.
Devdatt P. Dubhashi.
Complexity of Logical Theories.
September 1995.
x+46 pp.
Abstract: These are informal lecture notes from the course ``Fundamental Results of Complexity Theory'' taught at Aarhus University in the winter of 1994. The method of Ehrenfeucht-Fraïssé games is used to give a uniform framework for the analysis of the complexity of logical theories, following the well known monograph of Ferrante and Rackoff. Two examples are given as illustrations: the theory of real addition and the theory of Boolean algebras.

<

#257#>Contents
1
Introduction
1.1
Models, Languages and Theories
1.2
Decision Problems and their Complexity
1.3
Bibliographical Notes
2
Alternation
2.1
Alternating Turing Machines
2.2
Alternating Complexity Classes
2.3
Logical Theories in Alternating Classes
2.4
Bibliographical Notes
3
Ehrenfeucht-Fraïssé Games
3.1
Ehrenfeucht-Fraïssé Games and Elementary Equivalence
3.2
Ehrenfeucht-Fraïssé Games and Bounded Structures
3.3
Bibliographical Notes
4
Real Addition
4.1
Quantifier-Elimination
4.2
An EF Game
4.3
Lower Bound
4.4
A Research Problem
4.5
Bibliographical Notes
5
Boolean Algebras
5.1
The Structure of Boolean Algebras
5.2
Decision Procedures
5.3
Some Lower Bounds
5.4
Extensions
5.5
A Research Problem
5.6
Bibliographical Notes
.

LS-95-4
PostScript.
Dany Breslauer and Devdatt P. Dubhashi.
Combinatorics for Computer Scientists.
August 1995.
viii+184 pp.
Abstract: These are informal lecture notes from the course Combinatorics for Computer Scientists that was offered at Aarhus University in Spring 1995. The topics covered fall into roughly three parts corresponding to the organisation of these notes:

<

#282#>Contents
I
Enumeration
1
Inclusion-Exclusion
2
Inclusion-Exclusion II
3
Möbius Inversion
4
Möbius Inversion II
5
Generating Functions
6
Generating Functions II
7
Yet more on Generating Functions
8
Probability Generating Functions
9
A Coin Flipping Game
II
Graph Theory
10
Basics
11
Trees
12
Eulerian and Hamiltonian Walks
13
Connectivity
14
Matching
15
Edge Colouring
16
Cliques
17
Vertex Colouring
18
Planar Graphs
19
Problems
III
Linear Algebra in Combinatorics
20
Invitation to Club Theory
21
Some Club Theory Classics
22
More Club Theory
23
Greedy Algorithms and Matroids
24
Probability Spaces with Limited Independence
.

LS-95-3
PostScript, DVI.
Michael I. Schwartzbach.
Polymorphic Type Inference.
June 1995.
viii+24 pp.
Abstract: We will present a tiny functional language and gradually enrich its type system. We shall cover the basic Curry-Hindley system and Wand's constraint-based algorithm for monomorphic type inference; briefly observe the Curry-Howard isomorphism and notice that logical formalism may serve as the inspiration for new type rules; present the polymorphic Milner system and the Damas-Milner algorithm for polymorphic type inference; see the Milner-Mycroft system for polymorphic recursion; and sketch the development of higher type systems. We will touch upon the relationship between types and logic and show how rules from logic may give inspiration for new type rules. En route we shall encounter the curious discovery that two algorithmic problems for type systems, which have been implemented in popular programming languages, have turned out to be respectively complete for exponential time and undecidable.

<

#299#>Contents
1
Type Checking and Type Inference
2
A Tiny Functional Language
3
A Simple Type System
4
Simple Type Inference
5
Types and Logic
6
Polymorphic Types
7
Polymorphic Type Inference
8
Polymorphism and Recursion
9
Higher Type Systems
10
Problems
.

LS-95-2
PostScript, DVI.
Sven Skyum.
Introduction to Parallel Algorithms.
June 1995.
viii+17 pp. Second Edition.
Abstract: The material in this note is used as an introduction to parallel algorithms in a third year course on algorithms and complexity theory in Aarhus. Basic data structures and algorithms including sorting and searching are introduced to the students the first year. For the analysis of algorithms the unit cost model was used. The RAM were not introduced, the analysis was based on the number of operations in a (programming) language and corresponds to unit cost at a RAM.

This note covers an introduction to various PRAM's, presents Brents scheduling principle and various algorithms such as prefix, merging and sorting building up to a general method of simulating a CRCW-PRAM on a EREW-PRAM.

Two weeks are spent on the subject which corresponds to a total of six 45 minutes lectures.

The first version of the note was written in 1993 and was inspired by a note written by Peter Bro Miltersen the year before. Some of the problems originate from it. The note has since undergone revisions each year. Some of them have been substantial.

<

#310#>Contents
1
Models
2
Time, work and optimality
2.1
Brent's scheduling principle
3
Merging and Sorting
3.1
Prefix computations
3.2
Merging on a CRCW-PRAM
3.3
Bucketsort on an EREW-PRAM
4
Simulation of CRCW-PRAMs
5
Problems
.

LS-95-1
PostScript, DVI.
Jaap van Oosten.
Basic Category Theory.
January 1995.
vi+75 pp.
Abstract: This course was given to advanced undergraduate and beginning Ph.D. students in the fall of 1994 in Aarhus, as part of Glynn Winskel's semantics course. It is, in the author's view, the very minimum of category theory one needs to know if one is going to use it sensibly. Nevertheless, two topics are breathed on, which may be skipped: there is a glimpse of categorical logic, and there is a treatment of the $\lambda $-calculus in cartesian closed categories. These are there to give the reader at least a very rough idea of how the theory ``works''. The text contains a bit over hundred exercises, varying in difficulty, which supplement the treatment and are warmly recommended. There is an elaborate index.

<

#325#>Contents
1
Categories and Functors
1.1
Definitions and examples
1.2
Some special objects and arrows
2
Natural transformations
2.1
The Yoneda lemma
2.2
Examples of natural transformations
2.3
Equivalence of categories; an example
3
(Co)cones and (co)limits
3.1
Limits
3.2
Limits by products and equalizers
3.3
Colimits
4
A little piece of categorical logic
4.1
Regular categories and subobjects
4.2
Coherent logic in regular categories
4.3
The language 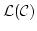$\cal L(C)$ and theory 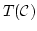$T(\cal C)$ associated to a regular category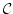 $\cal C$
4.4
Example of a regular category
5
Adjunctions
5.1
Adjoint functors
5.2
Expressing (co)completeness by existence of adjoints; preservation of (co)limits by adjoint functors
6
Monads and Algebras
6.1
Algebras for a monad
6.2
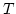$T$-Algebras at least as complete as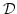 $\cal D$
6.3
The Kleisli category of a monad
7
Cartesian closed categories and the 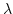$\lambda $-calculus
7.1
Cartesian closed categories (ccc's); examples and basic facts
7.2
Typed 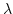$\lambda $-calculus and cartesian closed categories
7.3
Representation of primitive recursive functions in ccc's with natural numbers object
.

[BRICS symbol] BRICS WWW home page