Abstract:
This paper shows that the collection of identities which hold
in the algebra N of the natural numbers with constant zero, and binary
operations of sum and maximum is not finitely based. Moreover, it is proven
that, for every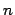 
, the equations in at most 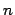variables that hold in
N do not form an equational basis. As a stepping stone in the proof of these
facts, several results of independent interest are obtained. In particular,
explicit descriptions of the free algebras in the variety generated by
N are offered. Such descriptions are based upon a geometric characterisation
of the equations that hold in N, which also yields that the equational
theory of N is decidable in exponential time
, the equations in at most variables that hold in
N do not form an equational basis. As a stepping stone in the proof of these
facts, several results of independent interest are obtained. In particular,
explicit descriptions of the free algebras in the variety generated by
N are offered. Such descriptions are based upon a geometric characterisation
of the equations that hold in N, which also yields that the equational
theory of N is decidable in exponential timeAvailable as PostScript, PDF, DVI.