Abstract:
The so-called weak König's lemma WKL asserts the existence
of an infinite path 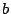 in any infinite binary tree (given by a representing
function
in any infinite binary tree (given by a representing
function 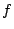 ). Based on this principle one can formulate subsystems of
higher-order arithmetic which allow to carry out very substantial parts of
classical mathematics but are
). Based on this principle one can formulate subsystems of
higher-order arithmetic which allow to carry out very substantial parts of
classical mathematics but are 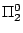 -conservative over primitive recursive
arithmetic PRA (and even weaker fragments of arithmetic). In 1992 we
established such conservation results relative to finite type extensions
PRA
-conservative over primitive recursive
arithmetic PRA (and even weaker fragments of arithmetic). In 1992 we
established such conservation results relative to finite type extensions
PRA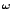 of PRA (together with a quantifier-free axiom of choice
schema). In this setting one can consider also a uniform version UWKL of WKL
which asserts the existence of a functional
of PRA (together with a quantifier-free axiom of choice
schema). In this setting one can consider also a uniform version UWKL of WKL
which asserts the existence of a functional 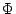 which selects uniformly in
a given infinite binary tree
which selects uniformly in
a given infinite binary tree 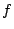 an infinite path
an infinite path 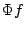 of that tree. This
uniform version of WKL is of interest in the context of explicit mathematics
as developed by S. Feferman. The elimination process from 1992 actually can
be used to eliminate even this uniform weak König's lemma provided that
PRA
of that tree. This
uniform version of WKL is of interest in the context of explicit mathematics
as developed by S. Feferman. The elimination process from 1992 actually can
be used to eliminate even this uniform weak König's lemma provided that
PRA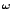 only has a quantifier-free rule of extensionality QF-ER
instead of the full axioms
only has a quantifier-free rule of extensionality QF-ER
instead of the full axioms 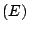 of extensionality for all finite types. In
this paper we show that in the presence of
of extensionality for all finite types. In
this paper we show that in the presence of 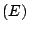 , UWKL is much stronger than
WKL: whereas WKL remains to be
, UWKL is much stronger than
WKL: whereas WKL remains to be 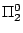 -conservative over PRA,
PRA
-conservative over PRA,
PRA
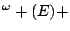 UWKL contains (and is conservative over) full Peano
arithmetic PA
UWKL contains (and is conservative over) full Peano
arithmetic PA
Available as PostScript, PDF, DVI.