Abstract:
A general class of languages for value-passing calculi based on
the late semantic approach is defined and a concrete instantiation of the
general syntax is given. This is a modification of the standard 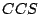 according to the late approach. Three kinds of semantics are given for this
language. First a Plotkin style operational semantics by means of an
applicative labelled transition system is introduced. This is a modification
of the standard labelled transition system that caters for value-passing
according to the late approach. As an abstraction, late bisimulation preorder
is given. Then a general class of denotational models for the late semantics
is defined. A denotational model for the concrete language is given as an
instantiation of the general class. Two equationally based proof systems are
defined. The first one, which is value-finitary, i. e. only reasons about a
finite number of values at each time, is shown to be sound and complete with
respect to this model. The second proof system, a value-infinitary one, is
shown to be sound with respect to the model, whereas the completeness is
proven later. The operational and the denotational semantics are compared and
it is shown that the bisimulation preorder is finer than the preorder induced
by the denotational model. We also show that in general the
according to the late approach. Three kinds of semantics are given for this
language. First a Plotkin style operational semantics by means of an
applicative labelled transition system is introduced. This is a modification
of the standard labelled transition system that caters for value-passing
according to the late approach. As an abstraction, late bisimulation preorder
is given. Then a general class of denotational models for the late semantics
is defined. A denotational model for the concrete language is given as an
instantiation of the general class. Two equationally based proof systems are
defined. The first one, which is value-finitary, i. e. only reasons about a
finite number of values at each time, is shown to be sound and complete with
respect to this model. The second proof system, a value-infinitary one, is
shown to be sound with respect to the model, whereas the completeness is
proven later. The operational and the denotational semantics are compared and
it is shown that the bisimulation preorder is finer than the preorder induced
by the denotational model. We also show that in general the
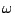 -bisimulation preorder is strictly included in the model induced
preorder. Finally a value-finitary version of the bisimulation preorder is
defined and the full abstractness of the denotational model with respect to
it is shown. It is also shown that for
-bisimulation preorder is strictly included in the model induced
preorder. Finally a value-finitary version of the bisimulation preorder is
defined and the full abstractness of the denotational model with respect to
it is shown. It is also shown that for 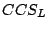 the
the 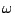 -bisimulation
preorder coincides with the preorder induced by the model. From this we can
conclude that if we allow for parameterized recursion in our language, we may
express processes which coincide in any algebraic domain but are
distinguished by the
-bisimulation
preorder coincides with the preorder induced by the model. From this we can
conclude that if we allow for parameterized recursion in our language, we may
express processes which coincide in any algebraic domain but are
distinguished by the 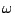 -bisimulation. This shows that if we extend
-bisimulation. This shows that if we extend
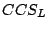 in this way we obtain a strictly more expressive
language
in this way we obtain a strictly more expressive
language
Available as PostScript, PDF, DVI.