Complexity of Weak Bisimilarity and Regularity for BPA and BPP

Jirí Srba

June 2000

Abstract:

It is an open problem whether weak bisimilarity is decidable for Basic Process Algebra (BPA) and Basic Parallel Processes (BPP). A PSPACE lower bound for BPA and NP lower bound for BPP have been demonstrated by Stribrna. Mayr achieved recently a result, saying that weak bisimilarity for BPP is 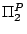$\Pi_2^P$-hard. We improve this lower bound to PSPACE, moreover for the restricted class of normed BPP.

Weak regularity (finiteness) of BPA and BPP is not known to be decidable either. In the case of BPP there is a $\Pi_2^P$-hardness result by Mayr, which we improve to PSPACE. No lower bound has previously been established for BPA. We demonstrate DP-hardness, which in particular implies both NP and co-NP-hardness.

In each of the bisimulation/regularity problems we consider also the classes of normed processes

Available as PostScript, PDF, DVI.

Last modified: 2003-06-08 by webmaster.