Foundational and Mathematical Uses of Higher Types

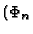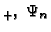In this paper we develop mathematically strong systems of analysis in higher types which, nevertheless, are proof-theoretically weak, i.e. conservative over elementary resp. primitive recursive arithmetic. These systems are based on non-collapsing hierarchies $(\Phi_n$ -WKL $_+, \ \Psi_n$ -WKL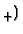

of principles which generalize (and for

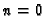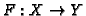coincide with) the so-called `weak' König's lemma WKL (which has been studied extensively in the context of second order arithmetic) to logically more complex tree predicates. Whereas the second order context used in the program of reverse mathematics requires an encoding of higher analytical concepts like continuous functions $F:X\rightarrow Y$ between Polish spaces

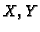, the more flexible language of our systems allows to treat such objects directly. This is of relevance as the encoding of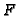

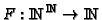used in reverse mathematics tacitly yields a constructively enriched notion of continuous functions which e.g. for $F:{\mathord{\rm I\mkern-3.1mu N}}^{{\mathord{\rm I\mkern-3.1mu N}}}\rightarrow{\mathord{\rm I\mkern-3.1mu N}}$ can be seen (in our higher order context) to be equivalent to the existence of a continuous modulus of pointwise continuity. For the direct representation of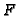

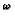the existence of such a modulus is independent even of full arithmetic in all finite types E-PA $^{\omega}$ plus quantifier-free choice, as we show using a priority construction due to L. Harrington. The usual WKL-based proofs of properties of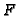

given in reverse mathematics make use of the enrichment provided by codes of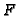

, and WKL does not seem to be sufficient to obtain similar results for the direct representation of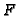

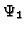in our setting. However, it turns out that $\Psi_1$ -WKL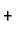

is sufficient.
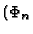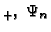Our conservation results for $(\Phi_n$ -WKL $_+, \ \Psi_n$ -WKL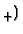

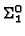are proved via a new elimination result for a strong non-standard principle of uniform $\Sigma^0_1$ -boundedness which we introduced in 1996 and which implies the WKL-extensions studied in this paper

Abstract: