Abstract:
For a system of polynomial equations over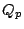 
we present an
efficient construction of a single polynomial of quite small degree whose
zero set over coincides with the zero set over of the original
system. We also show that the polynomial has some other attractive features
such as low additive and straight-line complexity.
we present an
efficient construction of a single polynomial of quite small degree whose
zero set over 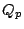coincides with the zero set over 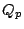of the original
system. We also show that the polynomial has some other attractive features
such as low additive and straight-line complexity.
The proof is based
on a link established here between the above problem and some recent number
theoretic result about zeros of 
-adic forms.
Available as PostScript, PDF, DVI.