Equational Axioms for Probabilistic Bisimilarity (Preliminary Report)

This paper gives an equational axiomatization of probabilistic bisimulation equivalence for a class of finite-state agents previously studied by Stark and Smolka ((2000) Proof, Language, and Interaction: Essays in Honour of Robin Milner, pp. 571-595). The axiomatization is obtained by extending the general axioms of iteration theories (or iteration algebras), which characterize the equational properties of the fixed point operator on (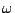 $\omega$ -)continuous or monotonic functions, with three axiom schemas that express laws that are specific to probabilistic bisimilarity. Hence probabilistic bisimilarity (over finite-state agents) has an equational axiomatization relative to iteration algebras

Abstract: