Abstract:
We define rationally additive semirings that are a
generalization of (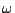
)complete and (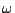-)continuous semirings.
We prove that every rationally additive semiring is an iteration semiring.
Moreover, we characterize the semirings of rational power series with
coefficients in 
, the semiring of natural numbers equipped with a
top element, as the free rationally additive semirings
)complete and (-)continuous semirings.
We prove that every rationally additive semiring is an iteration semiring.
Moreover, we characterize the semirings of rational power series with
coefficients in 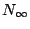, the semiring of natural numbers equipped with a
top element, as the free rationally additive semiringsAvailable as PostScript, PDF, DVI.