Abstract:
We present a calculus of proofs, the intended models of which
are categories with finite products and coproducts, initial algebras and
final coalgebras of functors that are recursively constructible out of these
operations, that is, 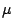 -bicomplete categories. The calculus satisfies the
cut elimination and its main characteristic is that the underlying graph of a
proof is allowed to contain a certain amount of cycles. To each proof of the
calculus we associate a system of equations which has a meaning in every
-bicomplete categories. The calculus satisfies the
cut elimination and its main characteristic is that the underlying graph of a
proof is allowed to contain a certain amount of cycles. To each proof of the
calculus we associate a system of equations which has a meaning in every
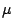 -bicomplete category. We prove that this system admits always a unique
solution, and by means of this theorem we define the semantics of the
calculus
-bicomplete category. We prove that this system admits always a unique
solution, and by means of this theorem we define the semantics of the
calculus
Available as PostScript, PDF, DVI.