Abstract:
We prove that AM (and hence Graph Nonisomorphism) is
in NP if for some 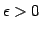 , some language in NE
, some language in NE
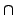 coNE requires nondeterministic circuits of size
coNE requires nondeterministic circuits of size
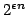 . This improves recent results of Arvind and Köbler and of Klivans and
Van Melkebeek who proved the same conclusion, but under stronger hardness
assumptions, namely, either the existence of a language in NE
. This improves recent results of Arvind and Köbler and of Klivans and
Van Melkebeek who proved the same conclusion, but under stronger hardness
assumptions, namely, either the existence of a language in NE
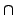 coNE which cannot be approximated by nondeterministic
circuits of size less than
coNE which cannot be approximated by nondeterministic
circuits of size less than
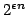 or the existence of a language in
NE
or the existence of a language in
NE 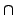 coNE which requires oracle circuits of
size
coNE which requires oracle circuits of
size
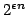 with oracle gates for SAT
(satisfiability).
with oracle gates for SAT
(satisfiability).
The previous results on derandomizing AM
were based on pseudorandom generators. In contrast, our approach is based on
a strengthening of Andreev, Clementi and Rolim's hitting set approach to
derandomization. As a spin-off, we show that this approach is strong enough
to give an easy (if the existence of explicit dispersers can be assumed
known) proof of the following implication: For some ![]() , if there is
a language in E which requires nondeterministic circuits of size
, if there is
a language in E which requires nondeterministic circuits of size
![]() , then P= BPP. This differs from
Impagliazzo and Wigderson's theorem ``only'' by replacing deterministic
circuits with nondeterministic ones
, then P= BPP. This differs from
Impagliazzo and Wigderson's theorem ``only'' by replacing deterministic
circuits with nondeterministic ones
Available as PostScript, PDF, DVI.