Super-Polynomial Versus Half-Exponential Circuit Size in the Exponential Hierarchy

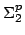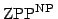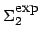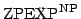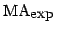Lower bounds on circuit size were previously established for functions in $\Sigma_2^p$ , ${\mbox{\rm ZPP}}^{\mbox{\rm\scriptsize NP}}$ , ${{\Sigma^{\mbox{\rm\small exp}}_2}}$ , ${{\mbox{\rm ZPEXP}}^{\mbox{\rm\scriptsize NP}}}$ and ${{\mbox{\rm MA}}_{\mbox{\rm\small exp}}}$ . We investigate the general question: Given a time bound

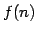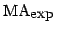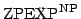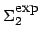. What is the best circuit size lower bound that can be shown for the classes ${\mbox{{\rm MA-TIME}}}[f]$ , ${\mbox{\rm ZP-TIME}}^ {\mbox{\rm\scriptsize NP}}[f], \ldots$ using the techniques currently known? For the classes ${{\mbox{\rm MA}}_{\mbox{\rm\small exp}}}$ , ${{\mbox{\rm ZPEXP}}^{\mbox{\rm\scriptsize NP}}}$ and ${{\Sigma^{\mbox{\rm\small exp}}_2}}$ , the answer we get is ``half-exponential''. Informally, a function

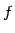is said to be half-exponential if

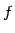composed with itself is exponential

Abstract: