On the Steiner Tree $\frac{3}{2}$-Approximation for Quasi-Bipartite Graphs

Romeo Rizzi

November 1999

Abstract:

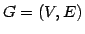
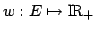
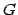
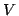
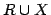
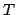
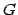
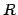
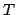
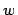
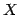
Let $G=(V,E)$ be an undirected simple graph and $w:E\mapsto {\rm I\!R}_+$ be a non-negative weighting of the edges of $G$. Assume $V$ is partitioned as $R\cup X$. A Steiner tree is any tree $T$ of $G$ such that every node in $R$ is incident with at least one edge of $T$. The metric Steiner tree problem asks for a Steiner tree of minimum weight, given that $w$ is a metric. 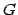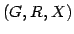When $X$ is a stable set of $G$, then $(G,R,X)$ is called quasi-bipartite. 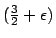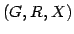In a SODA '99 paper, Rajagopalan and Vazirani introduced the notion of quasi-bipartiteness and gave a $(\frac{3}{2}+\epsilon)$ approximation algorithm for the metric Steiner tree problem, when $(G,R,X)$ is quasi-bipartite. In this paper, we simplify and strengthen the result of Rajagopalan and Vazirani. We also show how classical bit scaling techniques can be adapted to the design of approximation algorithms

Available as PostScript, PDF, DVI.

Last modified: 2003-06-08 by webmaster.