Linear Time Recognition of $P_4$-Indifferent Graphs

Romeo Rizzi

November 1999

Abstract:

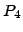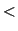
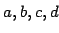
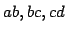
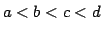
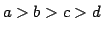
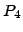
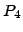
A simple graph is $P_4$ -indifferent if it admits a total order $<$ on its nodes such that every chordless path with nodes $a,b,c,d$ and edges $ab,bc,cd$ has $a<b<c<d$ or $a>b>c>d$. $P_4$-indifferent graphs generalize indifferent graphs and are perfectly orderable. Recently, Hoàng, Maffray and Noy gave a characterization of $P_4$-indifferent graphs in terms of forbidden induced subgraphs. 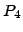We clarify their proof and describe a linear time algorithm to recognize $P_4$-indifferent graphs. 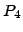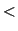When the input is a $P_4$-indifferent graph, then the algorithm computes an order $<$ as above

Available as PostScript, PDF.

Last modified: 2003-06-08 by webmaster.