Abstract:
It is shown that any sequence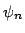 
of tautologies which
expresses the validity of a fixed combinatorial principle either is ``easy''
i.e. has polynomial size tree-resolution proofs or is ``difficult'' i.e
requires exponential size tree-resolution proofs. It is shown that the class
of tautologies which are hard (for tree-resolution) is identical to the class
of tautologies which are based on combinatorial principles which are violated
for infinite sets. Actually it is shown that the gap-phenomena is valid for
tautologies based on infinite mathematical theories (i.e. not just based on
a single proposition).
of tautologies which
expresses the validity of a fixed combinatorial principle either is ``easy''
i.e. has polynomial size tree-resolution proofs or is ``difficult'' i.e
requires exponential size tree-resolution proofs. It is shown that the class
of tautologies which are hard (for tree-resolution) is identical to the class
of tautologies which are based on combinatorial principles which are violated
for infinite sets. Actually it is shown that the gap-phenomena is valid for
tautologies based on infinite mathematical theories (i.e. not just based on
a single proposition).
We clarify the link between translating combinatorial principles (or more general statements from predicate logic) and the recent idea of using the symmetrical group to generate problems of propositional logic.
Finally, we show that is undecidable whether a
sequence (of the kind we consider) has polynomial size
tree-resolution proofs or requires exponential size tree-resolution proofs.
Also we show that the degree of the polynomial in the polynomial size (in
case it exists) is non-recursive, but semi-decidable.
Available as PostScript, PDF, DVI.