Abstract:
A temporal logic of causality (TLC) was introduced by Alur,
Penczek and Peled. It is basically a linear time temporal logic interpreted
over Mazurkiewicz traces which allows quantification over causal chains.
Through this device one can directly formulate causality properties of
distributed systems. In this paper we consider an extension of TLC by
strengthening the chain quantification operators. We show that our logic
TLC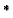
adds to the expressive power of TLC. We do so by defining an
Ehrenfeucht-Fraïssé game to capture the expressive power of TLC. We
then exhibit a property and by means of this game prove that the chosen
property is not definable in TLC. We then show that the same property is
definable in TLC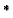. We prove in fact the stronger result that TLC 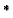is
expressively stronger than TLC exactly when the dependency relation
associated with the underlying trace alphabet is not
transitive.
adds to the expressive power of TLC. We do so by defining an
Ehrenfeucht-Fraïssé game to capture the expressive power of TLC. We
then exhibit a property and by means of this game prove that the chosen
property is not definable in TLC. We then show that the same property is
definable in TLC. We prove in fact the stronger result that TLC is
expressively stronger than TLC exactly when the dependency relation
associated with the underlying trace alphabet is not
transitive.Available as PostScript, PDF, DVI.