Experiments with ZF Set Theory in HOL and Isabelle

Most general purpose proof assistants support versions of typed higher order logic. Experience has shown that these logics are capable of representing most of the mathematical models needed in Computer Science. However, perhaps there exist applications where ZF-style set theory is more natural, or even necessary. 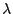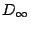Examples may include Scott's classical inverse-limit construction of a model of the untyped $\lambda$ -calculus ( $D_{\infty}$ ) and the semantics of parts of the Z specification notation. This paper compares the representation and use of ZF set theory within both HOL and Isabelle. 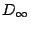The main case study is the construction of $D_{\infty}$ . The advantages and disadvantages of higher-order set theory versus first-order set theory are explored experimentally. This study also provides a comparison of the proof infrastructure of HOL and Isabelle.

Abstract: