Abstract:
Multi-exit iteration is a generalization of the standard binary
Kleene star operation that allows for the specification of agents that, up to
bisimulation equivalence, are solutions of systems of recursion equations of
the form
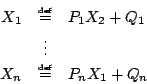
where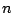 is a positive integer, and the
is a positive integer, and the 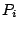 and the
and the 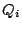 are process terms. The addition of multi-exit iteration to Basic Process
Algebra (BPA) yields a more expressive language than that obtained by
augmenting BPA with the standard binary Kleene star. This note offers an
expressiveness hierarchy, modulo bisimulation equivalence, for the family of
multi-exit iteration operators proposed by Bergstra, Bethke and
Ponse
are process terms. The addition of multi-exit iteration to Basic Process
Algebra (BPA) yields a more expressive language than that obtained by
augmenting BPA with the standard binary Kleene star. This note offers an
expressiveness hierarchy, modulo bisimulation equivalence, for the family of
multi-exit iteration operators proposed by Bergstra, Bethke and
Ponse
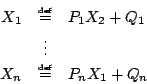
where
Available as PostScript, PDF, DVI.