Abstract:
A grove theory is a Lawvere algebraic theory 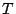 for which each
hom-set
for which each
hom-set 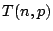 is a commutative monoid; composition on the right distrbutes
over all finite sums:
is a commutative monoid; composition on the right distrbutes
over all finite sums:
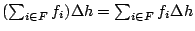 . A matrix theory is a grove theory in which composition on the left and
right distributes over finite sums. A matrix theory
. A matrix theory is a grove theory in which composition on the left and
right distributes over finite sums. A matrix theory 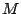 is isomorphic to a
theory of all matrices over the semiring
is isomorphic to a
theory of all matrices over the semiring 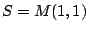 . Examples of grove
theories are theories of (bisimulation equivalence classes of)
synchronization trees, and theories of formal tree series over a semiring
. Examples of grove
theories are theories of (bisimulation equivalence classes of)
synchronization trees, and theories of formal tree series over a semiring
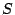 . Our main theorem states that if
. Our main theorem states that if 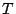 is a grove theory which has a matrix
subtheory
is a grove theory which has a matrix
subtheory 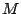 which is an iteration theory, then, under certain conditions,
the fixed point operation on
which is an iteration theory, then, under certain conditions,
the fixed point operation on 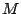 can be extended in exactly one way to a
fixedpoint operation on
can be extended in exactly one way to a
fixedpoint operation on 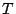 such that
such that 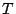 is an iteration theory. A second
theorem is a Kleene-type result. Assume that
is an iteration theory. A second
theorem is a Kleene-type result. Assume that 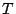 is a iteration grove theory
and
is a iteration grove theory
and 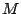 is a sub iteration grove theory of
is a sub iteration grove theory of 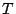 which is a matrix theory. For
a given collection
which is a matrix theory. For
a given collection 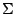 of scalar morphisms in
of scalar morphisms in 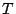 we describe the
smallest sub iteration grove theory of
we describe the
smallest sub iteration grove theory of 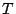 containing all the morphisms in
containing all the morphisms in
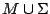
Available as PostScript, PDF, DVI.