Solving the String Statistics Problem in Time $O(n\log n)$

Gerth Stølting Brodal
Rune B. Lyngsø
Anna Östlin
Christian N. S. Pedersen

March 2002

Abstract:

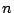
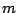
The string statistics problem consists of preprocessing a string of length $n$ such that given a query pattern of length $m$, the maximum number of non-overlapping occurrences of the query pattern in the string can be reported efficiently. 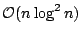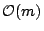Apostolico and Preparata introduced the minimal augmented suffix tree (MAST) as a data structure for the string statistics problem, and showed how to construct the MAST in time ${\cal O}(n\log^2 n)$ and how it supports queries in time ${\cal O}(m)$ for constant sized alphabets. A subsequent theorem by Fraenkel and Simpson stating that a string has at most a linear number of distinct squares implies that the MAST requires space ${\cal O}(n)$. 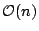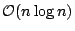In this paper we improve the construction time for the MAST to ${\cal O}(n\log n)$ by extending the algorithm of Apostolico and Preparata to exploit properties of efficient joining and splitting of search trees together with a refined analysis

Available as PostScript, PDF, DVI.

Last modified: 2003-06-08 by webmaster.