Abstract:
A vertex set 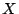 of a digraph
of a digraph 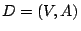 is a kernel if
is a kernel if
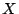 is independent (i.e., all pairs of distinct vertices of
is independent (i.e., all pairs of distinct vertices of 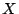 are
non-adjacent) and for every
are
non-adjacent) and for every 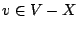 there exists
there exists 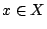 such that
such that 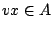 . A vertex set
. A vertex set 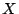 of a digraph
of a digraph 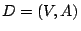 is a quasi-kernel if
is a quasi-kernel if 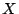 is
independent and for every
is
independent and for every 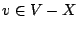 there exist
there exist
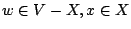 such that
either
such that
either 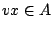 or
or 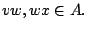 In 1994, Chvátal and Lovász proved that
every digraph has a quasi-kernel. In 1996, Jacob and Meyniel proved that, if
a digraph
In 1994, Chvátal and Lovász proved that
every digraph has a quasi-kernel. In 1996, Jacob and Meyniel proved that, if
a digraph 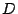 has no kernel, then
has no kernel, then 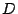 contains at least three quasi-kernels.
We characterize digraphs with exactly one and two quasi-kernels, and, thus,
provide necessary and sufficient conditions for a digraph to have at least
three quasi-kernels. In particular, we prove that every strong digraph of
order at least three, which is not a 4-cycle, has at least three
quasi-kernels. We conjecture that every digraph with no sink has a pair of
disjoint quasi-kernels and provide some support to this
conjecture
contains at least three quasi-kernels.
We characterize digraphs with exactly one and two quasi-kernels, and, thus,
provide necessary and sufficient conditions for a digraph to have at least
three quasi-kernels. In particular, we prove that every strong digraph of
order at least three, which is not a 4-cycle, has at least three
quasi-kernels. We conjecture that every digraph with no sink has a pair of
disjoint quasi-kernels and provide some support to this
conjecture
Available as PostScript, PDF, DVI.