Abstract:
Computational experiments show that the greedy algorithm (GR)
and the nearest neighbor algorithm (NN), popular choices for tour
construction heuristics, work at acceptable level for the Euclidean TSP, but
produce very poor results for the general Symmetric and Asymmetric TSP (STSP
and ATSP). We prove that for every 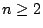 there is an instance of ATSP
(STSP) on
there is an instance of ATSP
(STSP) on 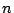 vertices for which GR finds the worst tour. The same result
holds for NN. We also analyze the repetitive NN (RNN) that starts NN from
every vertex and chooses the best tour obtained. We prove that, for the ATSP,
RNN always produces a tour, which is not worse than at least
vertices for which GR finds the worst tour. The same result
holds for NN. We also analyze the repetitive NN (RNN) that starts NN from
every vertex and chooses the best tour obtained. We prove that, for the ATSP,
RNN always produces a tour, which is not worse than at least 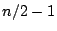 other
tours, but for some instance it finds a tour, which is not worse than at most
other
tours, but for some instance it finds a tour, which is not worse than at most
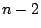 other tours,
other tours, 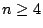 . We also show that, for some instance of the STSP
on
. We also show that, for some instance of the STSP
on 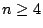 vertices, RNN produces a tour not worse than at most
vertices, RNN produces a tour not worse than at most 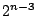 tours. These results are in sharp contrast to earlier results by G. Gutin and
A. Yeo, and A. Punnen and S. Kabadi, who proved that, for the ATSP, there are
tour construction heuristics, including some popular ones, that always build
a tour not worse than at least
tours. These results are in sharp contrast to earlier results by G. Gutin and
A. Yeo, and A. Punnen and S. Kabadi, who proved that, for the ATSP, there are
tour construction heuristics, including some popular ones, that always build
a tour not worse than at least 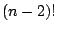 tours
tours
Available as PostScript, PDF, DVI.