Abstract:
We define the degree of aperiodicity of finite automata and
show that for every set 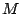 of positive integers, the class
of positive integers, the class 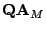 of
finite automata whose degree of aperiodicity belongs to the division ideal
generated by
of
finite automata whose degree of aperiodicity belongs to the division ideal
generated by 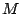 is closed with respect to direct products, disjoint unions,
subautomata, homomorphic images and renamings. These closure conditions
define q-varieties of finite automata. We show that q-varieties are in a
one-to-one correspondence with literal varieties of regular languages. We
also characterize
is closed with respect to direct products, disjoint unions,
subautomata, homomorphic images and renamings. These closure conditions
define q-varieties of finite automata. We show that q-varieties are in a
one-to-one correspondence with literal varieties of regular languages. We
also characterize 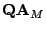 as the cascade product of a variety of
counters with the variety of aperiodic (or counter-free) automata. We then
use the notion of degree of aperiodicity to characterize the expressive power
of first-order logic and temporal logic with cyclic counting with respect to
any given set
as the cascade product of a variety of
counters with the variety of aperiodic (or counter-free) automata. We then
use the notion of degree of aperiodicity to characterize the expressive power
of first-order logic and temporal logic with cyclic counting with respect to
any given set 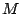 of moduli. It follows that when
of moduli. It follows that when 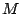 is finite, then it is
decidable whether a regular language is definable in first-order or temporal
logic with cyclic counting with respect to moduli in
is finite, then it is
decidable whether a regular language is definable in first-order or temporal
logic with cyclic counting with respect to moduli in 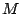
Available as PostScript, PDF, DVI.