On Weak Markov's Principle

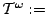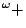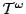We show that the so-called weak Markov's principle (WMP) which states that every pseudo-positive real number is positive is underivable in ${\cal T}^{\omega}:=$ E-HA $^{\omega}+$ AC. Since ${\cal T}^{\omega}$ allows to formalize (at least large parts of) Bishop's constructive mathematics this makes it unlikely that WMP can be proved within the framework of Bishop-style mathematics (which has been open for about 20 years). 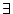The underivability even holds if the ineffective schema of full comprehension (in all types) for negated formulas (in particular for $\exists$ -free formulas) is added which allows to derive the law of excluded middle for such formulas.

Abstract: