Abstract:
This paper studies the equational theory of various exotic
semirings presented in the literature. Exotic semirings are semirings whose
underlying carrier set is some subset of the set of real numbers equipped
with binary operations of minimum or maximum as sum, and addition as product.
Two prime examples of such structures are the 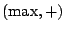 semiring and
the tropical semiring. It is shown that none of the exotic semirings
commonly considered in the literature has a finite basis for its equations,
and that similar results hold for the commutative idempotent weak semirings
that underlie them. For each of these commutative idempotent weak semirings,
the paper offers characterizations of the equations that hold in them,
decidability results for their equational theories, explicit descriptions of
the free algebras in the varieties they generate, and relative axiomatization
results
semiring and
the tropical semiring. It is shown that none of the exotic semirings
commonly considered in the literature has a finite basis for its equations,
and that similar results hold for the commutative idempotent weak semirings
that underlie them. For each of these commutative idempotent weak semirings,
the paper offers characterizations of the equations that hold in them,
decidability results for their equational theories, explicit descriptions of
the free algebras in the varieties they generate, and relative axiomatization
results
Available as PostScript, PDF, DVI.