Abstract:
We study the fundamental problem of sorting 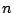 integers of
integers of 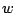 bits on a unit-cost RAM with word size
bits on a unit-cost RAM with word size 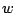 , and in particular consider the
time-space trade-off (product of time and space in bits) for this problem.
For comparison-based algorithms, the time-space complexity is known to be
, and in particular consider the
time-space trade-off (product of time and space in bits) for this problem.
For comparison-based algorithms, the time-space complexity is known to be
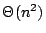 . A result of Beame shows that the lower bound also holds for
non-comparison-based algorithms, but no algorithm has met this for time below
the comparison-based
. A result of Beame shows that the lower bound also holds for
non-comparison-based algorithms, but no algorithm has met this for time below
the comparison-based
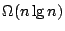 lower bound.
lower bound.
We show that if
sorting within some time bound ![]() is possible, then time
is possible, then time
![]() can be achieved with high probability using space
can be achieved with high probability using space
![]() , which is optimal. Given a deterministic priority queue using
amortized time
, which is optimal. Given a deterministic priority queue using
amortized time ![]() per operation and space
per operation and space ![]() , we provide a
deterministic algorithm sorting in time
, we provide a
deterministic algorithm sorting in time
![]() with
with
![]() . Both results require that
. Both results require that
![]() . Using
existing priority queues and sorting algorithms, this implies that we can
deterministically sort time-space optimally in time
. Using
existing priority queues and sorting algorithms, this implies that we can
deterministically sort time-space optimally in time ![]() for
for
![]() , and with high probability for
, and with high probability for
![]() .
.
Our
results imply that recent lower bounds for deciding element distinctness in
![]() time are nearly tight
time are nearly tight
Available as PostScript, PDF, DVI.