Abstract:
We investigate the time complexity of constructing single input
double output state feedback controller structures, given the directed
structure graph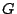 
of a system. Such a controller structure defines a
restricted type of 
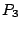-partition of the graph 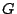. A necessary condition
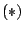has been found and two classes of graphs have been identified where the
search problem of finding a feasible 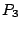-partition is polynomially solvable
and, in addition, 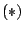is not only necessary but also sufficient for the
existence of a 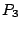-partition. It is shown further that the decision problem
on two particular graph classes -- defined in terms of forbidden subgraphs
-- remains NP-complete, but is polynomially solvable on the
intersection of those two classes. Moreover, for every natural number 
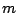, a
stabilizing structure with Single Input 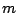-Output controllers can be found
in polynomial time for the system in question, if it admits one
of a system. Such a controller structure defines a
restricted type of -partition of the graph . A necessary condition
has been found and two classes of graphs have been identified where the
search problem of finding a feasible -partition is polynomially solvable
and, in addition, is not only necessary but also sufficient for the
existence of a -partition. It is shown further that the decision problem
on two particular graph classes -- defined in terms of forbidden subgraphs
-- remains NP-complete, but is polynomially solvable on the
intersection of those two classes. Moreover, for every natural number , a
stabilizing structure with Single Input -Output controllers can be found
in polynomial time for the system in question, if it admits oneAvailable as PostScript, PDF.