A
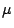
-lattice is a lattice with the property that every unary
polynomial has both a least and a greatest fix-point. In this paper we define
the quasivariety of
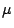
-lattices and, for a given partially ordered set
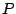
, we construct a
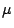
-lattice
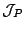
whose elements are
equivalence classes of games in a preordered class
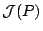
. We prove
that the
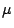
-lattice
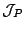
is free over the ordered set
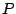
and
that the order relation of
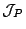
is decidable if the order
relation of
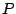
is decidable. By means of this characterization of free
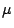
-lattices we infer that the class of complete lattices generates the
quasivariety of
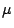
-lattices