A Tough Nut for Tree Resolution

Stefan Dantchev
Søren Riis

May 2000

Abstract:

One of the earliest proposed hard problems for theorem provers is a propositional version of the Mutilated Chessboard problem. It is well known from recreational mathematics: Given a chessboard having two diagonally opposite squares removed, prove that it cannot be covered with dominoes. In Proof Complexity, we consider not ordinary, but 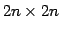$2n\times 2n$ mutilated chessboard. In the paper, we show a 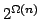$2^{\Omega \left( n\right) }$ lower bound for tree resolution.

Available as PostScript, PDF.

Last modified: 2003-06-08 by webmaster.