This document is also available as
PostScript
and
DVI.
- NS-96-15
-
PostScript,
DVI.
CoFI.
CASL - The CoFI Algebraic Specification Language; Tentative
Design: Language Summary.
December 1996.
34 pp.
Abstract: The Common Framework Initiative (CoFI) for algebraic
specification and development is an international collaborative effort,
coordinated by Peter D. Mosses. This summary of the tentative design of the
CoFI Algebraic Specification Language, CASL, is the basis for closer
investigation by various CoFI task groups (Semantics, Tools, Methodology,
Language Design), after which a final CASL Design Proposal will be made in
Spring 1997.
The language CASL is central to CoFI: it is a reasonably
expressive algebraic language for specifying requirements and design for
conventional software. From CASL, simpler CoFI languages (e.g., for
interfacing with existing tools) are to be obtained by restriction, and CASL
is to be incorporated in more advanced CoFI languages (e.g., for specifying
reactive systems). CASL strikes a balance between simplicity and
expressiveness.
- NS-96-14
-
PostScript,
DVI.
Peter D. Mosses.
A Tutorial on Action Semantics.
December 1996.
46 pp. Tutorial notes for FME '94 (Formal Methods Europe, Barcelona,
1994) and FME '96 (Formal Methods Europe, Oxford, 1996).
Abstract: Action Semantics is useful for specifying programming
languages: documenting design decisions, setting standards for
implementations, etc. This framework has unusually good pragmatics, making
specifications easily accessible to programmers. Thanks to its inherent
modularity, action semantics scales up smoothly to describing practical,
industrially-useful languages.
In this 1/2-day tutorial, action
semantics is explained, illustrated, and compared to other frameworks such as
VDM and RAISE.
- NS-96-13
-
Olivier Danvy, editor.
Proceedings of the Second ACM SIGPLAN Workshop on Continuations,
CW '97 (ENS, Paris, France, 14 January, 1997), December 1996.
166 pp.
Abstract: The notion of continuation is ubiquitous in many
different areas of computer science, including logic, constructive
mathematics, programming languages, and programming. This workshop aims at
providing a forum for discussion of new results and work in progress; work
aimed at a better understanding of the nature of continuations; applications
of continuations, and the relation of continuations to other areas of logic
and computer science.
CW '97 is taking place on January 14th, 1997,
the day preceding POPL '97. It consists of two invited talks by Peter Landin
and by John Reynolds, and seven contributed papers. The present BRICS
technical report (distributed at the workshop) serves as an informal
proceedings. Seven papers were selected among eighteen submissions.
- NS-96-12
-
Mandayam K. Srivas.
A Combined Approach to Hardware Verification: Proof-Checking,
Rewriting with Decision Procedures and Model-Checking; Part II: Articles.
BRICS Autumn School on Verification.
October 1996.
56 pp.
Abstract: The notes consists of the following articles:
- (1)
- Modular Verification of SRT Division, by H. Ruess,
N. Shankar, and M.K. Srivas. Presented at CAV '96, Springer Verlag LNCS 1102,
pp. 123-134, July 1996, New Brunswick, NJ.
- (2)
- An Integration of
Model-Checking with Automated Proof Checking, by S. Rajan, N. Shankar, and
M.K. Srivas. Presented at the Conference on Computer-Aided Verification,
CAV '95, Liege, Belgium, July 1995. Springer Verlag Lecture Notes in Computer
Science vol. 939, pp. 84-97.
- (3)
- Effective Theorem Proving for
Hardware Verification, by David Cyrluk, S. Rajan, N. Shankar, and M. K.
Srivas, presented at the 2nd International Conference on Theorem Provers in
Circuit Design, September 1994.
.
- NS-96-11
-
Mandayam K. Srivas.
A Combined Approach to Hardware Verification: Proof-Checking,
Rewriting with Decision Procedures and Model-Checking; Part I: Slides.
BRICS Autumn School on Verification.
October 1996.
29 pp.
Abstract: Slides to lectures on A Combined Approach to
Hardware Verification: Proof-Checking, Rewriting with Decision Procedures and
Model-Checking. See BRICS Notes NS-96-12.
- NS-96-10
-
Robert Pollack.
What we Learn from Formal Checking; Part III: Formalization is
Not Just Filling In Details. BRICS Autumn School on Verification.
October 1996.
iv+42 pp.
Abstract: I outline a small example in LEGO, a formal
development of basic lambda calculus. Some ``obvious'' theorems appear to be
very difficult to prove, in that their conventional informal proofs are not
easily formalizable. I show a method using generalized induction that makes
these ``obvious'' theorems straightfoward. The moral is that a user of formal
checking must be willing to solve new problems, that formalization can teach
us new things about ``well understood'' areas, and that using alternative
definitions of basic concepts is one way to learn these new things.
- NS-96-9
-
Robert Pollack.
What we Learn from Formal Checking; Part II: Using Type
Theory: An Introduction. BRICS Autumn School on Verification.
October 1996.
iv+71 pp.
Abstract: An introduction to the Curry-Howard isomorphism and
the use of type theory for representing mathematics and modelling computer
systems. I will concentrate on the Extended Calculus of Constructions (ECC)
of Luo, and on the tool LEGO for checking proofs in ECC. The main technical
topic is the use of inductive definitions to represent data types (booleans,
natural numbers, lists, syntax of a programming language, ...) and
relations (typing and operational semantics of a programming language,
...).
Acknowledgement This section was written by Rod Bur
stall and Judith Underwood.
- NS-96-8
-
Robert Pollack.
What we Learn from Formal Checking; Part I: How to Believe a
Machine-Checked Proof. BRICS Autumn School on Verification.
October 1996.
iv+19 pp.
Abstract: There has been considerable discussion about the
value of a large machine-checked proof. I suggest a view, and a technical
approach, in which belief in machine verifications is based on evidence,
which may be built up over time, and requires participation of the readers. I
split the question of belief into two parts; asking whether the claimed proof
is actually a derivation in the claimed formal system, and then whether what
it proves is the claimed theorem. The first question is addressed by
independent checking of formal proofs. I discuss how this approach extends
the informal notion of proof as surveyable by human readers, and how
surveyability of proofs reappears as the issue of feasibility of
proof-checking. The second question has no technical answer.
- NS-96-7
-
Tom F. Melham.
Some Research Issues in Higher Order Logic Theorem Proving.
BRICS Autumn School on Verification.
October 1996.
15 pp.
Abstract: The past twenty years have seen many advances in the
use of computers to do logical proofs and in the deployment of this
technology in what, broadly speaking, might be called formal methods
applications. One important strand has been research in interactive
proof-construction in higher-order logics, where the user guides proof
discovery and construction but may also employ automatic decision procedures
or heuristics. Several well-developed theorem-proving systems (e.g. HOL,
Isabelle, Coq, Nuprl) serve as vehicles for this research; and the results of
past work have begun to reach industry through, for example, the notable
recent achievements in hardware verification using PVS and the use of HOL at
several industrial sites.
These lectures focus on three important
areas for future research in interactive higher order logic theorem proving:
- Usability and interface design.
- Embedding
formalisms and embedded theorem proving.
- Integrating and implementing
automated proof methods.
Concentrating primarily on research
issues, I shall discuss some past and current work in these areas and sketch
what I see as some important directions for the future. In keeping with the
aims of the BRICS Autumn School on Verification, I have in mind an audience
of beginning Ph.D. students or newly-appointed RAs--i.e. researchers who
may be familiar with some aspects of theorem proving, but who want to expand
their knowledge a little. Experienced researchers, deeply versed in higher
order logic theorem proving, are likely to find some of what I say already
familiar to them.
- NS-96-6
-
Gerard J. Holzmann.
On-the-Fly Model Checking Tutorial. BRICS Autumn School on
Verification.
October 1996.
31 pp.
Abstract: SPIN is a generic verification system for models of
distributed software systems. It has been used to detect design errors in
applications ranging from abstract distributed algorithms, to detailed code
for controlling telephone exchanges. This paper gives an overview of the
design and structure of the verifier, reviews its automata-theoretical
foundation, and gives examples of some typical applications of the model
checker in practice.
- NS-96-5
-
Thomas A. Henzinger.
Automatic Verification of Real-Time and Hybrid Systems. BRICS
Autumn School on Verification.
October 1996.
28 pp.
Abstract: We summarize several recent resul ts about hybrid
automata. Our goal is to demonstrate that concepts from the theory of
discrete concurrent systems can give insights into partly continuous systems,
and that methods for the verification of finite-state systems can be used to
analyze certain systems with uncountable state spaces.
- NS-96-4
-
Edmund M. Clarke, Jr.
Symbolic Model Checking. BRICS Autumn School on Verification.
October 1996.
55 pp.
Abstract: Logical errors in finite state reactive systems are
an important problem for designers. They can delay getting a new product on
the market or cause the failure of some critical device that is already in
use. My research group has developed a verification method called temporal logic model checking for this class of systems. In this approach
specifications are expressed in a propositional temporal logic, and reactive
systems are modeled as state-transition graphs. An efficient search
procedure is used to determine automatically if the specifications are
satisfied by the state-transition graph. The technique has been used in the
past to find subtle errors in a number of non-trivial circuit and protocol
designs.
During the last few years, the size of the reactive systems
that can be verified by model checking techniques has increased dramatically.
By representing sets of states and transition relations implicitly using
Binary Decision Diagrams (BDDs), we are now able to check examples that are
many orders of magnitude larger than was previously the case. In this
tutorial we describe how the BDD-based model checking techniques work and
illustrate their power by discussing the verification of several complex
protocol and circuit designs.
- NS-96-3
-
David A. Basin.
Verification Based on Monadic Logic. BRICS Autumn School on
Verification.
October 1996.
43 pp.
Abstract: We present a new approach to hardware verification
based on describing circuits in Monadic Second-order Logic MSL. We show how
to use this logic to represent generic designs like 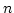 -bit adders, which are
parameterized in space, and sequential circuits, where time is an unbounded
parameter. MSL admits a decision procedure, implemented in the MONA tool,
which reduces formulas to canonical automata. -bit adders, which are
parameterized in space, and sequential circuits, where time is an unbounded
parameter. MSL admits a decision procedure, implemented in the MONA tool,
which reduces formulas to canonical automata.
The decision problem for
MSL is non-elementary decidable and thus unlikely to be usable in practice.
However, we have used MONA to automatically verify, or find errors in, a
number of circuits studied in the literature. Previously published machine
proofs of the same circuits are based on deduction and may involve
substantial interaction with the user. Moreover, our approach is orders of
magnitude faster for the examples considered. We show why the underlying
computations are feasible and how our use of MONA generalizes standard
BDD-based hardware reasoning.
- NS-96-2
-
PostScript.
Allan Cheng, Kim G. Larsen, and Mogens
Nielsen, editors.
Programme and Abstracts of the BRICS Autumn School on
Verification (Aarhus, Denmark, October 28 - November 1, 1996), August
1996.
ii+18pp.
Abstract: This note is intended to provide helpful information,
including Scientific Programme with Abstracts, concerning attendance to the
BRICS Autumn School on Verification, Aarhus, Denmark, October 28 -
November 1, 1996.
- NS-96-1
-
PostScript.
André Berthiaume.
Quantum Computation. Mini-Course.
January 1996.
iv+126 pp.
Abstract: Computer science has a classical soul; many
definitions implicitly contain ideas from the time we believed the world
evolved according to newtonian physics. Ideas such as: an object's state is
well defined, instantaneous actions at a distance are impossible, etc. Modern
physics and more specifically quantum physics tells us that Nature is not as
straightforward as Newton originally believed. One can prepare systems such
that the state is completely undefined in any classical sense. Instantaneous
actions at a distance have been observed and sometimes having less
alternatives to produce a given outcome may improve the probability
of getting this outcome! What would happen computing models are allowed to
operate within the rules of quantum physics? What are the advantages offered
by a quantum computer?
This mini-course introduces the quantum
computer and presents some of the milestone results in quantum complexity
theory leading up to Shor's famous polynomial time quantum factoring
algorithm. Foreknowledge of quantum physics is useful but not necessary as
the relevant notions are introduced when needed. A fascinating aspect of
quantum computation is the possibility of building such devices. Some of the
problems still to be overcome will briefly addressed, but it is worth
mentioning that some ongoing experiments have shown some very positive
results. Quantum computers may well be available sooner than we think.
|
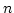 -bit adders, which are
parameterized in space, and sequential circuits, where time is an unbounded
parameter. MSL admits a decision procedure, implemented in the MONA tool,
which reduces formulas to canonical automata.
-bit adders, which are
parameterized in space, and sequential circuits, where time is an unbounded
parameter. MSL admits a decision procedure, implemented in the MONA tool,
which reduces formulas to canonical automata.