Abstract:
We determine the computational complexity of the dynamic convex
hull problem in the planar case. We present a data structure that maintains a
finite set of points in the plane under insertion and deletion of points in
amortized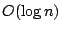 
time. Here n denotes the number of points in the set.
The data structure supports the reporting of the extreme point of the set in
some direction in worst-case and amortized time. The space usage
of the data structure is 
. We give a lower bound on the amortized
asymptotic time complexity that matches the performance of this data
structure
time. Here n denotes the number of points in the set.
The data structure supports the reporting of the extreme point of the set in
some direction in worst-case and amortized 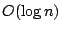time. The space usage
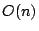of the data structure is . We give a lower bound on the amortized
asymptotic time complexity that matches the performance of this data
structureAvailable as PostScript, PDF.