Abstract:
Some alternative characterizations of late full congruences,
either strong or weak, are presented. Those congruences are classically
defined by requiring the corresponding ground bisimilarity under all name
substitutions. We first improve on those infinitary definitions by
showing that congruences can be alternatively characterized in the
 -calculus by sticking to a finite number of carefully identified
substitutions, and hence, by resorting to only a finite number of ground
bisimilarity checks. -calculus by sticking to a finite number of carefully identified
substitutions, and hence, by resorting to only a finite number of ground
bisimilarity checks. Then we investigate the same issue in both the
ground and the non-ground 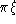 -calculus, a CCS-like process algebra whose
ground version has already been proved to coincide with ground -calculus, a CCS-like process algebra whose
ground version has already been proved to coincide with ground
 -calculus. The -calculus. The 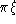 -calculus perspective allows processes to be
explicitly interpreted as functions of their free names. As a result, a
couple of alternative characterizations of -calculus perspective allows processes to be
explicitly interpreted as functions of their free names. As a result, a
couple of alternative characterizations of  -congruences are given, each
of them in terms of the bisimilarity of one single pair of -congruences are given, each
of them in terms of the bisimilarity of one single pair of
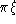 -processes. In one case, we exploit -processes. In one case, we exploit 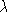 -closures of processes,
so inducing the effective generation of the substitutions necessary to infer
non-ground equivalence. In the other case, a more promising call-by-need
discipline for the generation of the wanted substitutions is used. This last
strategy is also adopted to show a coincidence result with open
semantics. -closures of processes,
so inducing the effective generation of the substitutions necessary to infer
non-ground equivalence. In the other case, a more promising call-by-need
discipline for the generation of the wanted substitutions is used. This last
strategy is also adopted to show a coincidence result with open
semantics. By minor changes, all of the above characterizations for
late semantics can be suited for congruences of the early
family
Available as PostScript,
PDF,
DVI.
|