Abstract:
In [Kreisel 51],[Kreisel 52] G. Kreisel introduced the
no-counterexample interpretation (n.c.i.) of Peano arithmetic. In particular
he proved, using a complicated 
-substitution method (due to W.
Ackermann), that for every theorem A (A prenex) of first-order Peano
arithmetic PA one can find ordinal recursive functionals
of order type 
which realize the
Herbrand normal form 
of A.
Subsequently more perspicuous
proofs of this fact via functional interpretation (combined with
normalization) and cut-elimination where found. These proofs however do not
carry out the n.c.i. as a local proof interpretation and don't respect
the modus ponens on the level of the n.c.i. of formulas A and
. Closely related to this phenomenon is the fact that both
proofs do not establish the condition 
and - at least not
constructively - 
which are part of the definition of an
`interpretation of a formal system' as formulated in [Kreisel 51].
In this paper we determine the complexity of the n.c.i. of the modus ponens rule for
- (i)
- PA-provable sentences,
- (ii)
- for arbitrary sentences
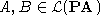uniformly in functionals satisfying the n.c.i. of (prenex normal forms of)
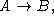A and 
and - (iii)
- for arbitrary 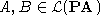pointwise in given
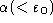-recursive
functionals satisfying the n.c.i. of A and .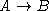
.Finally we discuss a
variant of the concept of an interpretation presented in [Kreisel 58] and
show that it is incomparable with the concept studied in [Kreisel
51],[Kreisel 52]. In particular we show that the n.c.i. of PA
by
-recursive functionals (
) is an
interpretation in the sense of [Kreisel 58] but not in the sense of [Kreisel
51] since it violates the condition
Available as PostScript, PDF, DVI.