Abstract:
In this paper we study the logic 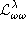 , which is first order logic extended by
quantification over functions (but not over relations). We give the syntax of
the logic, as well as the semantics in Heyting categories with exponentials.
Embedding the generic model of a theory into a Grothendieck topos yields
completeness of , which is first order logic extended by
quantification over functions (but not over relations). We give the syntax of
the logic, as well as the semantics in Heyting categories with exponentials.
Embedding the generic model of a theory into a Grothendieck topos yields
completeness of 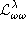 with respect to models in
Grothendieck toposes, which can be sharpened to completeness with respect to
Heyting valued models. The logic with respect to models in
Grothendieck toposes, which can be sharpened to completeness with respect to
Heyting valued models. The logic 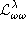 is the
strongest for which Heyting valued completeness is known. Finally, we relate
the logic to locally connected geometric morphisms between
toposes is the
strongest for which Heyting valued completeness is known. Finally, we relate
the logic to locally connected geometric morphisms between
toposes
Available as PostScript,
PDF,
DVI.
|