Abstract:
Fokkink ((1994) Inf. Process. Lett. 52: 333-337)
has recently proposed a complete equational axiomatization of strong
bisimulation equivalence for the language obtained by extending Milner's
basic CCS with prefix iteration. Prefix iteration is a variation on the
original binary version of the Kleene star operation 
obtained by
restricting the first argument to be an atomic action. In this paper, we
extend Fokkink's results to a setting with the unobservable action 
by
giving a complete equational axiomatization of Milner's observation
congruence over Fokkink's language. The axiomatization is obtained by
extending Fokkink's axiom system with two of Milner's standard -laws
and the following three equations that describe the interplay between the
silent nature of and prefix iteration:
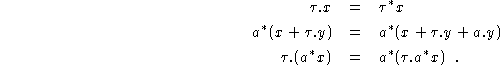
Using a technique due
to Groote, we also show that the resulting axiomatization is
-complete, i.e., complete for equality of open terms.
Available as PostScript, PDF, DVI.