In this master's thesis we present a modal logic for Applied
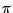
which characterises observational equivalence on processes. The
motivation is similar to that of Applied
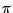
itself, namely generality: the
logic can be adapted to a particular application simply by defining a
suitable equational theory on terms.
As a first step towards the logic
for Applied 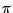 , a strong version of static equivalence on frames is
introduced in which term reductions are observable in addition to equality on
terms. We argue that the strong version is meaningful in applications and
give two refined definitions based on the notion of cores introduced in work
by Boreale et al. for the Spi calculus. The refined definitions are useful
because they do not involve universal quantification over arbitrary terms and
hence are amenable to a logical characterisation. We show that the refined
definitions coincide with the original definition of strong static
equivalence under certain general conditions.
, a strong version of static equivalence on frames is
introduced in which term reductions are observable in addition to equality on
terms. We argue that the strong version is meaningful in applications and
give two refined definitions based on the notion of cores introduced in work
by Boreale et al. for the Spi calculus. The refined definitions are useful
because they do not involve universal quantification over arbitrary terms and
hence are amenable to a logical characterisation. We show that the refined
definitions coincide with the original definition of strong static
equivalence under certain general conditions.
A first order logic for
frames which characterises strong static equivalence and which yields
characteristic formulae is then given based on the refined definitions of
strong static equivalence. This logic facilitates direct reasoning about
terms in a frame as well as indirect reasoning about knowledge deducible from
a frame. The logic for Applied 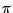 is then obtained by adding suitable
Hennessy-Milner style modalities to the logic for frames, hence facilitating
reasoning about both static and dynamic properties of processes. We finally
demonstrate the logic with an application to the analysis of the
Needham-Schroeder Public Key Protocol
is then obtained by adding suitable
Hennessy-Milner style modalities to the logic for frames, hence facilitating
reasoning about both static and dynamic properties of processes. We finally
demonstrate the logic with an application to the analysis of the
Needham-Schroeder Public Key Protocol