Abstract:
In this paper we review the known bounds for 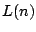 , the
circuit size complexity of the hardest Boolean function on
, the
circuit size complexity of the hardest Boolean function on 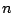 input bits.
The best known bounds appear to be
input bits.
The best known bounds appear to be
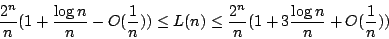
However, the bounds do not seem to be explicitly stated in the literature. We give a simple direct elementary proof of the lower bound valid for the full binary basis, and we give an explicit proof of the upper bound valid for the basis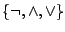
However, the bounds do not seem to be explicitly stated in the literature. We give a simple direct elementary proof of the lower bound valid for the full binary basis, and we give an explicit proof of the upper bound valid for the basis
Available as PostScript, PDF, DVI.