Abstract:
We present algorithms for finding a longest common increasing
subsequence of two or more input sequences. For two sequences of lengths 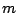 and
and 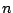 , where
, where 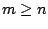 , we present an algorithm with an output-dependent
expected running time of
, we present an algorithm with an output-dependent
expected running time of
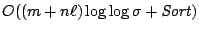 and
and
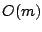 space, where
space, where 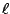 is the length of a LCIS,
is the length of a LCIS, 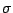 is the size of
the alphabet, and
is the size of
the alphabet, and 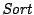 is the time to sort each input
sequence.For
is the time to sort each input
sequence.For 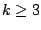 length-
length-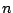 sequences we present an algorithm
running time
sequences we present an algorithm
running time
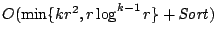 , which improves the
previous best bound by more than a factor
, which improves the
previous best bound by more than a factor 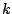 for many inputs. In both cases,
our algorithms are conceptually quite simple but rely on existing
sophisticated data structures.Finally, we introduce the problem of
longest common weakly-increasing (or non-decreasing) subsequences (LCWIS),
for which we present an
for many inputs. In both cases,
our algorithms are conceptually quite simple but rely on existing
sophisticated data structures.Finally, we introduce the problem of
longest common weakly-increasing (or non-decreasing) subsequences (LCWIS),
for which we present an 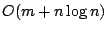 time algorithm for the 3-letter
alphabet case. For the extensively studied Longest Common Subsequence
problem, comparable speedups have not been achieved for small
alphabets.
time algorithm for the 3-letter
alphabet case. For the extensively studied Longest Common Subsequence
problem, comparable speedups have not been achieved for small
alphabets.
Available as PostScript, PDF, DVI.