On the Adaptiveness of Quicksort

Quicksort was first introduced in 1961 by Hoare. Many variants have been developed, the best of which are among the fastest generic sorting algorithms available, as testified by the choice of Quicksort as the default sorting algorithm in most programming libraries. Some sorting algorithms are adaptive, i.e. they have a complexity analysis which is better for inputs which are nearly sorted, according to some specified measure of presortedness. 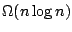Quicksort is not among these, as it uses $\Omega(n \log n)$ comparisons even when the input is already sorted. However, in this paper we demonstrate empirically that the actual running time of Quicksort is adaptive with respect to the presortedness measure $\Inv$ . Differences close to a factor of two are observed between instances with low and high $\Inv$ value. We then show that for the randomized version of Quicksort, the number of element swaps performed is provably adaptive with respect to the measure $\Inv$ . 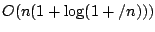More precisely, we prove that randomized Quicksort performs expected $O(n(1+\log (1+\Inv/n)))$ element swaps, where $\Inv$ denotes the number of inversions in the input sequence. This result provides a theoretical explanation for the observed behavior, and gives new insights on the behavior of the Quicksort algorithm. We also give some empirical results on the adaptive behavior of Heapsort and Mergesort

Abstract: