Abstract:
Inspired by the Maximum Satisfiability and Exact Satisfiability
problems we present two Maximum Exact Satisfiability problems. The first
problem called Maximum Exact Satisfiability is: given a formula in
conjunctive normal form and an integer 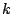 , is there an assignment to all
variables in the formula such that at least
, is there an assignment to all
variables in the formula such that at least 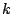 clauses have exactly one true
literal. The second problem called Restricted Maximum Exact Satisfiability
has the further restriction that no clause is allowed to have more than one
true literal. Both problems are proved NP-complete restricted to the versions
where each clause contains at most two literals. In fact Maximum Exact
Satisfiability is a generalisation of the well-known NP-complete problem
MaxCut. We present an exact algorithm for Maximum Exact Satisfiability where
each clause contains at most two literals with time complexity
clauses have exactly one true
literal. The second problem called Restricted Maximum Exact Satisfiability
has the further restriction that no clause is allowed to have more than one
true literal. Both problems are proved NP-complete restricted to the versions
where each clause contains at most two literals. In fact Maximum Exact
Satisfiability is a generalisation of the well-known NP-complete problem
MaxCut. We present an exact algorithm for Maximum Exact Satisfiability where
each clause contains at most two literals with time complexity
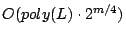 , where
, where 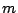 is the number of clauses and
is the number of clauses and 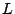 is the length of
the formula. For the second version we give an algorithm with time complexity
is the length of
the formula. For the second version we give an algorithm with time complexity
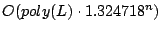 , where
, where 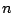 is the number of variables. We note
that when restricted to the versions where each clause contains exactly two
literals and there are no negations both problems are fixed parameter
tractable. It is an open question if this is also the case for the general
problems.
is the number of variables. We note
that when restricted to the versions where each clause contains exactly two
literals and there are no negations both problems are fixed parameter
tractable. It is an open question if this is also the case for the general
problems.
Available as PostScript, PDF.