Abstract:
We present an Extended Quadratic Frobenius Primality Test
(EQFT), which is related to the Miller-Rabin test and the Quadratic Frobenius
test (QFT) by Grantham. EQFT takes time about equivalent to 2 Miller-Rabin
tests, but has much smaller error probability, namely 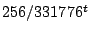 for
for 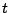 iterations of the test in the worst case. EQFT extends QFT by verifying
additional algebraic properties related to the existence of elements of order
dividing 24. We also give bounds on the average-case behaviour of the test:
consider the algorithm that repeatedly chooses random odd
iterations of the test in the worst case. EQFT extends QFT by verifying
additional algebraic properties related to the existence of elements of order
dividing 24. We also give bounds on the average-case behaviour of the test:
consider the algorithm that repeatedly chooses random odd 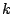 bit numbers,
subjects them to
bit numbers,
subjects them to 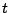 iterations of our test and outputs the first one found
that passes all tests. We obtain numeric upper bounds for the error
probability of this algorithm as well as a general closed expression bounding
the error. For instance, it is at most
iterations of our test and outputs the first one found
that passes all tests. We obtain numeric upper bounds for the error
probability of this algorithm as well as a general closed expression bounding
the error. For instance, it is at most 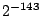 for
for 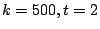 . Compared
to earlier similar results for the Miller-Rabin test, the results indicates
that our test in the average case has the effect of 9 Miller-Rabin tests,
while only taking time equivalent to about 2 such tests. We also give bounds
for the error in case a prime is sought by incremental search from a random
starting point
. Compared
to earlier similar results for the Miller-Rabin test, the results indicates
that our test in the average case has the effect of 9 Miller-Rabin tests,
while only taking time equivalent to about 2 such tests. We also give bounds
for the error in case a prime is sought by incremental search from a random
starting point
Available as PostScript, PDF.