Abstract:
We present simple and efficient algorithms for computing gcd
and cubic residuosity in the ring of Eisenstein integers,
![${\bf Z}[\zeta]$](Abs/img1.gif) ,
i.e. the integers extended with
,
i.e. the integers extended with 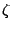 , a complex primitive third root of
unity. The algorithms are similar and may be seen as generalisations of the
binary integer gcd and derived Jacobi symbol algorithms. Our algorithms take
time
, a complex primitive third root of
unity. The algorithms are similar and may be seen as generalisations of the
binary integer gcd and derived Jacobi symbol algorithms. Our algorithms take
time 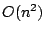 for
for 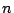 bit input. This is an improvement from the known
results based on the Euclidian algorithm, and taking time
bit input. This is an improvement from the known
results based on the Euclidian algorithm, and taking time 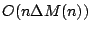 ,
where
,
where 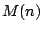 denotes the complexity of multipliplying
denotes the complexity of multipliplying 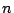 bit integers. The
new algorithms have applications in practical primality tests and the
implementation of cryptographic protocols. The technique underlying our
algorithms can be used to obtain equally fast algorithms for gcd and quartic
residuosity in the ring of Gaussian integers,
bit integers. The
new algorithms have applications in practical primality tests and the
implementation of cryptographic protocols. The technique underlying our
algorithms can be used to obtain equally fast algorithms for gcd and quartic
residuosity in the ring of Gaussian integers, ![${\bf Z}[i]$](Abs/img7.gif)
Available as PostScript, PDF, DVI.