On converting CNF to DNF

We study how big the blow-up in size can be when one switches between the CNF and DNF representations of boolean functions. For a function 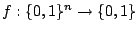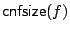$f:\{0,1\}^n \rightarrow \{0,1\}$ , $\mbox{\sf cnfsize}(f)$ denotes the minimum number of clauses in a CNF for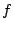

; similarly, 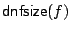$\mbox{\sf dnfsize}(f)$ denotes the minimum number of terms in a DNF for

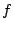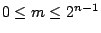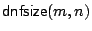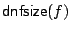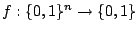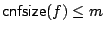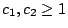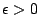. For $0\leq m \leq 2^{n-1}$ , let $\mbox{\sf dnfsize}(m,n)$ be the maximum $\mbox{\sf dnfsize}(f)$ for a function $f:\{0,1\}^n \rightarrow \{0,1\}$ with $\mbox{\sf cnfsize}(f) \leq m$ . We show that there are constants $c_1,c_2 \geq 1$ and $\epsilon > 0$ , such that for all large

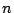and all $m \in [ \frac{1}{\epsilon}n,2^{\epsilon{n}}]$ , we have

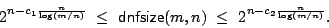
$\begin{displaymath}2^{n - c_1\frac{n}{\log(m/n)}}~ \leq~\mbox{\sf dnfsize}(m,n) ~\leq~ 2^{n-c_2 \frac{n}{\log(m/n)}}.\end{displaymath}$

In particular, when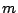

is the polynomial

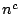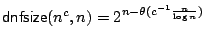, we get $\mbox{\sf dnfsize}(n^c,n) = 2^{n -\theta(c^{-1}\frac{n}{\log n})}$ .

Abstract: