A Denotational Account of Untyped Normalization by Evaluation

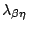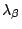We show that the standard normalization-by-evaluation construction for the simply-typed $\lambda_{\beta\eta}$ -calculus has a natural counterpart for the untyped $\lambda_\beta$ -calculus, with the central type-indexed logical relation replaced by a ``recursively defined'' invariant relation, in the style of Pitts. In fact, the construction can be seen as generalizing a computational-adequacy argument for an untyped, call-by-name language to normalization instead of evaluation.

In the untyped setting, not all terms have normal forms, so the normalization function is necessarily partial. We establish its correctness in the senses of soundness (the output term, if any, is $\beta$ -equivalent to the input term); standardization ( $\beta$ -equivalent terms are mapped to the same result); and completeness (the function is defined for all terms that do have normal forms). We also show how the semantic construction enables a simple yet formal correctness proof for the normalization algorithm, expressed as a functional program in an ML-like call-by-value language.

Abstract: