Abstract:
Carrying out a suggestion by Kreisel, we adapt Gödel's
functional interpretation to ordinary first-order predicate logic(PL) and
thus devise an algorithm to extract Herbrand terms from PL-proofs. The
extraction is carried out in an extension of PL to higher types. The
algorithm consists of two main steps: first we extract a functional realizer,
next we compute the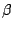 
-normal-form of the realizer from which the
Herbrand terms can be read off. Even though the extraction is carried out in
the extended language, the terms are ordinary PL-terms. In contrast to
approaches to Herbrand's theorem based on cut elimination or
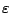-elimination this extraction technique is, except for the
normalization step, of low polynomial complexity, fully modular and
furthermore allows an analysis of the structure of the Herbrand terms, in the
spirit of Kreisel, already prior to the normalization step. It is expected
that the implementation of functional interpretation in Schwichtenberg's
MINLOG system can be adapted to yield an efficient Herbrand-term extraction
tool.
-normal-form of the realizer from which the
Herbrand terms can be read off. Even though the extraction is carried out in
the extended language, the terms are ordinary PL-terms. In contrast to
approaches to Herbrand's theorem based on cut elimination or
-elimination this extraction technique is, except for the
normalization step, of low polynomial complexity, fully modular and
furthermore allows an analysis of the structure of the Herbrand terms, in the
spirit of Kreisel, already prior to the normalization step. It is expected
that the implementation of functional interpretation in Schwichtenberg's
MINLOG system can be adapted to yield an efficient Herbrand-term extraction
tool.Available as PostScript, PDF, DVI.