New Algorithms for Exact Satisfiability

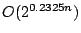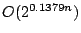The Exact Satisfiability problem is to determine if a CNF-formula has a truth assignment satisfying exactly one literal in each clause; Exact 3-Satisfiability is the version in which each clause contains at most three literals. In this paper, we present algorithms for Exact Satisfiability and Exact 3-Satisfiability running in time $O(2^{0.2325n})$ and $O(2^{0.1379n})$ , respectively. 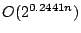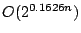The previously best algorithms have running times $O(2^{0.2441n})$ for Exact Satisfiability (Monien, Speckenmeyer and Vornberger (1981)) and $O(2^{0.1626n})$ for Exact 3-Satisfiability (Kulikov and independently Porschen, Randerath and Speckenmeyer (2002)). We extend the case analyses of these papers and observe, that a formula not satisfying any of our cases has a small number of variables, for which we can try all possible truth assignments and for each such assignment solve the remaining part of the formula in polynomial time.

Abstract: