Abstract:
We show new lower and upper bounds on the number of maximal
induced bipartite subgraphs of graphs with 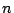 vertices. We present an
infinite family of graphs having
vertices. We present an
infinite family of graphs having
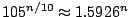 such
subgraphs, which improves an earlier lower bound by Schiermeyer (1996). We
show an upper bound of
such
subgraphs, which improves an earlier lower bound by Schiermeyer (1996). We
show an upper bound of
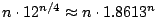 and give an
algorithm that lists all maximal induced bipartite subgraphs in time
proportional to this bound. This is used in an algorithm for checking
4-colourability of a graph running within the same time bound
and give an
algorithm that lists all maximal induced bipartite subgraphs in time
proportional to this bound. This is used in an algorithm for checking
4-colourability of a graph running within the same time bound
Available as PostScript, PDF.