Abstract:
We show that the number of maximal independent sets of size
exactly 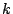 in any graph of size
in any graph of size 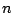 is at most
is at most
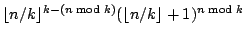 . For maximal
independent sets of size at most
. For maximal
independent sets of size at most 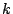 the same bound holds for
the same bound holds for 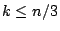 . For
. For 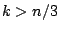 a bound of approximately
a bound of approximately 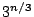 is given. All the bounds
are exactly tight and improve Eppstein (2001) who give the bound
is given. All the bounds
are exactly tight and improve Eppstein (2001) who give the bound
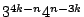 on the number of maximal independent sets of size at most
on the number of maximal independent sets of size at most
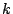 , which is the same for
, which is the same for
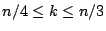 , but larger otherwise. We
give an algorithm listing the maximal independent sets in a graph in time
proportional to these bounds (ignoring a polynomial factor), and we use this
algorithm to construct algorithms for 4- and 5- colouring running in time
, but larger otherwise. We
give an algorithm listing the maximal independent sets in a graph in time
proportional to these bounds (ignoring a polynomial factor), and we use this
algorithm to construct algorithms for 4- and 5- colouring running in time
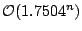 and
and
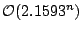 , respectively
, respectively
Available as PostScript, PDF, DVI.