Abstract:
In this paper we argue for an extension of the second order
framework currently used in the program of reverse mathematics to finite
types. In particular we propose a conservative finite type extension
RCA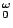 of the second order base system RCA
of the second order base system RCA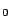 . By this
conservation nothing is lost for second order statements if we reason in
RCA
. By this
conservation nothing is lost for second order statements if we reason in
RCA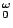 instead of RCA
instead of RCA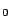 . However, the presence of finite types
allows to treat various analytical notions in a rather direct way, compared
to the encodings needed in RCA
. However, the presence of finite types
allows to treat various analytical notions in a rather direct way, compared
to the encodings needed in RCA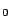 which are not always provably faithful in
RCA
which are not always provably faithful in
RCA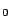 . Moreover, the language of finite types allows to treat many more
principles and gives rise to interesting extensions of the existing scheme of
reverse mathematics. We indicate this by showing that the class of principles
equivalent (over RCA
. Moreover, the language of finite types allows to treat many more
principles and gives rise to interesting extensions of the existing scheme of
reverse mathematics. We indicate this by showing that the class of principles
equivalent (over RCA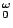 ) to Feferman's non-constructive
) to Feferman's non-constructive
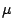 -operator forms a mathematically rich and very robust class. This is
closely related to a phenomenon in higher type recursion theory known as
Grilliot's trick
-operator forms a mathematically rich and very robust class. This is
closely related to a phenomenon in higher type recursion theory known as
Grilliot's trick
Available as PostScript, PDF, DVI.