One of the most well-known induction principles in computer
science is the fixed point induction rule, or least pre-fixed point rule.
Inductive
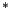
-semirings are partially ordered semirings equipped with a star
operation satisfying the fixed point equation and the fixed point induction
rule for linear terms. Inductive
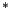
-semirings are extensions of continuous
semirings and the Kleene algebras of Conway and Kozen.
We develop, in
a systematic way, the rudiments of the theory of inductive 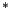 -semirings in
relation to automata, languages and power series. In particular, we prove
that if
-semirings in
relation to automata, languages and power series. In particular, we prove
that if 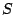 is an inductive
is an inductive 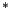 -semiring, then so is the semiring of
matrices
-semiring, then so is the semiring of
matrices
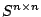 , for any integer
, for any integer 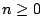 , and that if
, and that if 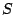 is an
inductive
is an
inductive 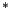 -semiring, then so is any semiring of power series
-semiring, then so is any semiring of power series
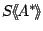 . As shown by Kozen, the
dual of an inductive
. As shown by Kozen, the
dual of an inductive 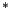 -semiring may not be inductive. In contrast, we show
that the dual of an iteration semiring is an iteration semiring. Kuich proved
a general Kleene theorem for continuous semirings, and Bloom and Ésik
proved a Kleene theorem for all Conway semirings. Since any inductive
-semiring may not be inductive. In contrast, we show
that the dual of an iteration semiring is an iteration semiring. Kuich proved
a general Kleene theorem for continuous semirings, and Bloom and Ésik
proved a Kleene theorem for all Conway semirings. Since any inductive
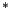 -semiring is a Conway semiring and an iteration semiring, as we show,
there results a Kleene theorem applicable to all inductive
-semiring is a Conway semiring and an iteration semiring, as we show,
there results a Kleene theorem applicable to all inductive 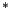 -semirings. We
also describe the structure of the initial inductive
-semirings. We
also describe the structure of the initial inductive 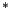 -semiring and
conjecture that any free inductive
-semiring and
conjecture that any free inductive 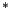 -semiring may be given as a semiring
of rational power series with coefficients in the initial inductive
-semiring may be given as a semiring
of rational power series with coefficients in the initial inductive
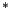 -semiring. We relate this conjecture to recent axiomatization results on
the equational theory of the regular sets
-semiring. We relate this conjecture to recent axiomatization results on
the equational theory of the regular sets